Pythonで理解する蟻本(プログラミングコンテストチャレンジブック)
この記事のコンセプト
プログラミングコンテストチャレンジブック(以下蟻本)は競技プログラミングの参考書として圧倒的な知名度を誇っており、まさに競技プログラマーにとっての必需品といえます。
その一方で、蟻本のコードはすべてC++で書かれており、Pythonで競技プログラミングをしている人にとってはコードの理解が困難なものになっています。
蟻本を理解するためにC++を学ぶのも一つの手ではありますが、それだけで多大な労力が必要となってしまいます。
そこでこの記事では、Pythonコーダーが蟻本を理解する際の補助となるように、蟻本のコードをできるだけ忠実にPythonで書き直したものを記載しようと思います。
この記事が、Pythonコーダーが蟻本を理解する一助となれば幸いです。
記事一覧
1 いざチャレンジ!でもその前に―準備編
1-1 プログラミングコンテストって何?
2 基礎からスタート!―初級編
2-1 すべての基本”全探索”
2-2 猪突猛進!”貪欲法”
2-3 値を覚えて再利用”動的計画法”
2-4 データを工夫して記憶する”データ構造”
2-5 あれもこれも実は”グラフ”
2-6 数学的な問題を解くコツ
3 ここで差がつく!―中級編
3-1 値の検索だけじゃない!"二分探索"
非情報系が応用情報に合格する方法
こんにちは、クルトンです!
2023年4月16日に実施された、応用情報に合格することができました!
なので合格するまでにやった事をこの記事にまとめておこうと思います。
勉強を始める前の状態
- その他の情報系の知識は全く無い(大学は情報系の学部ではなく、基本情報も受けていないのでマジで何も知らなかった)
という感じでした。アルゴリズムの知識が有ったのは午後試験において有利だったと思いますが、それ以外のことはすべて応用情報のテキストを使って勉強しました。
参考書
使用した参考書やサイトを所要時間と個人的なおススメ度を5段階で紹介します。
応用情報技術者合格教本
所要時間:17時間(3割ぐらい読みました)
おススメ度:★★☆☆☆
感想:説明が難しくて全然読み進められませんでした。
範囲の隅々までカバーしているのは良い所ですが、合わないと思ったら途中でもテキストを変えることをお勧めします。
基本情報技術者合格教本
所要時間:14時間(4割ぐらい読みました)
おススメ度:★★☆☆☆
感想:応用情報の合格教本が難しかったので、基本情報の知識が足りないから難しく感じるのかなと思い基本情報の合格教本を買いました。
結局合格教本シリーズの説明が僕に合っていなかっただけだったので、こちらも読み切る事はできませんでした。
キタミ式イラストIT塾 応用情報技術者
所要時間:42時間(2周しました)
おススメ度:★★★★★
感想:とても分かりやすかったです。図解や具体的な説明が多く、平易な文章で書かれているのでスラスラ読めました。
ただ、午前試験では一部キタミ式に載っていないことも問われるので注意が必要です(これに関しては後述します)。
応用情報技術者 午後問題の重点
所要時間:20時間(分野によって異なりますが、大体3,4回分ぐらい解きました)
おススメ度:★★★★☆
感想:午後試験の問題集です。解説がしっかりしているのでおススメです。
勉強のポイント
応用情報を勉強する際に、個人的に重要だと思った事を書こうと思います。
合わないと思ったらテキストを変える
合わないテキストで勉強するのはツラいので、読んでいる途中でも思い切って変えちゃいましょう(大量にテキストを買っておいて全部途中までしか読んでない、とかはマズいかも知れないけど)。
僕の場合はキタミ式がとても合っていたので、テキストを変えてから勉強がかなり楽になりました。
キタミ式は意外と午前試験の範囲をカバーできてない
これは過去問を解くと分かりますが、午前試験ではキタミ式に載っていなかったことが割と出題されます。
これらの範囲の勉強は、過去問演習で解けなかった問題の解説を読むだけで充分だと思います。
ただ、キタミ式さえ完璧にすれば大丈夫!と勝手に思っていて、過去問演習をせずに試験を受けると6割ギリギリになってしまうかもしれないので気を付けましょう。
過去問を早くからやる
この記事で一番伝えたかった事です。本当に過去問は早くから解いておいた方が良いです。
理由は
- 問題数が多いため時間がかかる
- 午前試験は過去問がそのまま流用されている
という2点です。
問題数が多いため時間がかかる
まず、過去問演習にかかる時間について説明します。
1回の試験時間は午前試験(150分)+午後試験(150分)で計5時間です。
本番で少し時間が余るように演習しておきたいことを考えると過去問演習の時間は3~4時間が理想でしょう。
復習する時間も考えると全部で7時間ぐらいかかると思います。普通に1日潰れちゃいますね。
当然ながら過去問の解答や復習の速度に個人差はあるとおもいますが、1回分の演習にかなりの時間がかかることは知っておくと良いと思います。
午前試験は過去問がそのまま流用されている
次に、午前試験に過去問がそのまま流用されていることについてです。具体的な問題数についてですが、80問中半分の40問程が問題文、選択肢を全く変えることなくそのまま流用されています(データはここから確認できます)。
また、問題が流用は直近の試験からだけでなく、かなり前の試験からもされているため、午前試験に関しては過去問は解きすぎて損という事はありません。
以上の理由から、早い段階から過去問演習を進めておくことをお勧めします。
最後に
応用情報は勉強方法についての解説記事が多かったので、他の人が触れていなさそうな部分で伝えたい事だけを書きました。
この記事が誰かのお役に立てれば幸いです。
BERTによるツイートのいいね数予測とLIMEによる判断根拠の可視化
この記事はでぶ Advent Calendar 2022 10日目の記事です。
こんにちは、クルトンです!
この記事ではデブさんのツイートを用いて、ツイート内容といいね数の相関について調べた結果を書いていこうと思います。
この記事を書くに至ったきっかけ
殆どの方はご存じかと思いますが、念のために書いておくとデブさんは😡界隈の第一人者として有名なツイッタラーです。
そのツイートの多くには大量の😡が含まれています。

そこで僕は「😡系インフルエンサーのデブさんなら😡を多くすればするほどいいね数が増えるのではないか?」という仮説を立てました。
そのため、この記事ではデブさんのツイートを分析し、😡がいいね数に与える影響について調べようと思います。
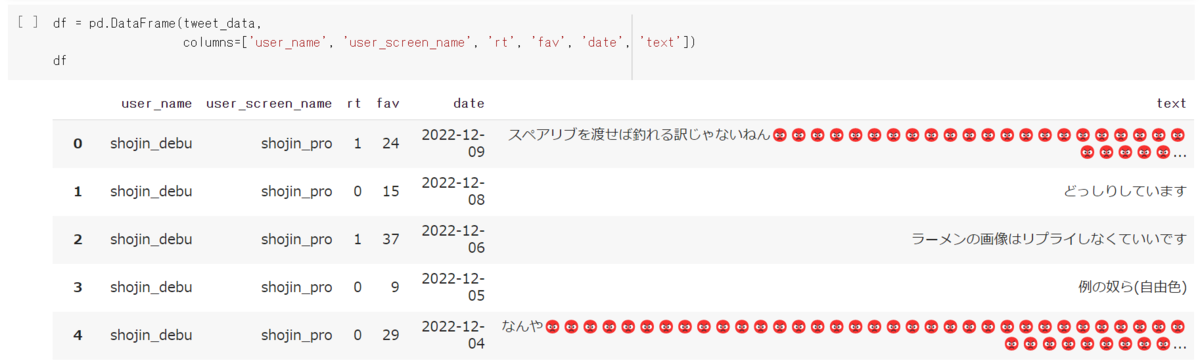
TwitterAPIでツイートを取得する
まずTwitter API v2を用いてデブさんのツイートを取得します。
Twitter API v2にはEssential, Elevated, Academic Researchの3つのアクセスレベルがあります。
今回は他人のツイートを取得しなければならないので、デフォルトのEssentialではなくElevated プランを用いました。
(ElevatedプランはEssentialプランとは異なり申請が必要ですが、無料で使うことができます。)
リプライと元のツイートではいいね数に差があると考え、今回はリプライではないツイートのみを収集しました。
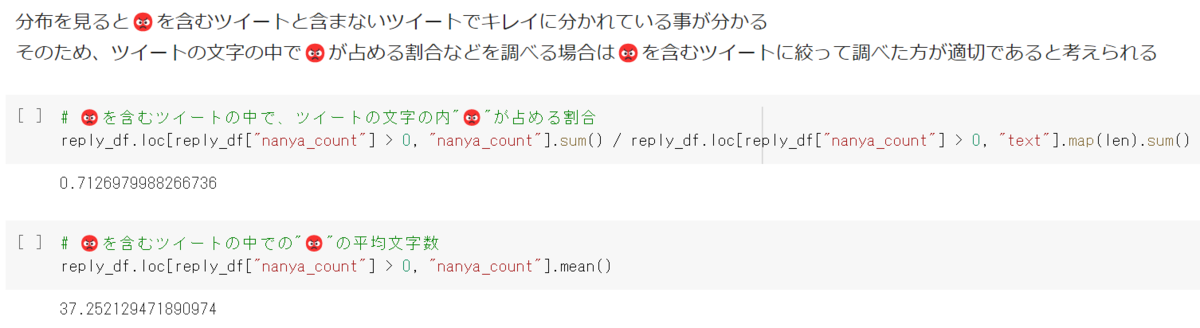
簡単なEDA
まずは😡を含むツイートの割合を調べてみましょう。

予想に反してかなり小さい値が返ってきました。意外に😡を含んでいるツイートは少ないようです。
では次にいいね数と😡の関係性を可視化してみましょう
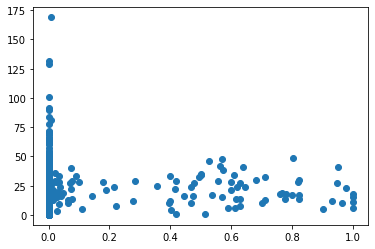
図は縦軸がいいね数、横軸がツイートの文字のうち😡が占める割合です。
…図を見る限りあまり関係性が無さそうにみえます。
次に、いいね順に並べたときの上位10件と下位10件のツイートの内容を見てみましょう


良いね数の下位10件はこれといって特徴がありませんが、上位10件にはABCの成績ツイートが多い事が分かります(10分の3がABCのコンテスト成績ツイート)。
競プロアカウントなのでこれは自然な結果と言えるでしょう。
BERTによっていいね数を予測し、判断根拠をLIMEによって可視化する
次に、LIMEを使ってどの部分がツイートの伸びに影響を与えているかについて分析したいと思います。
LIME(Local Interpretable Model-agnostic Explainations)とは、複雑なモデルを単純な線形回帰で近似することで解釈性の向上を目指す手法です。
BERTなどの複雑なモデルがどのようなところを判断基準にしているかを可視化して解釈する際に用いることができます。
今回はLIMEのLimeTextExplainerというものを使うのですが、これが回帰に対応していませんでした。
そのため今回は、いいね数を上位30%と下位30%の二つの集団に分け、2値分類タスクとしてBERTに解かせようと思います。
その後、学習済みBERTの判断根拠をLimeTextExplainerによって可視化して、ツイートのどの部分がツイートが伸びるか伸びないかに影響しているのかを調べてみました。
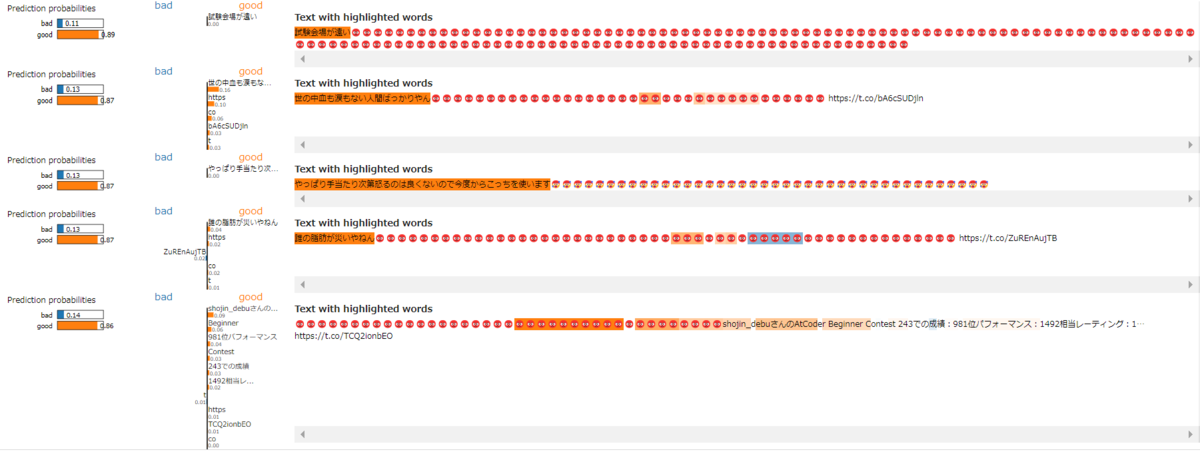

オレンジの線が引かれた部分がいいね数が多くなるとBERTが判断した要素、青色の線が引かれた部分がいいね数が少なくなるとBERTが判断した要素です。
図を見る限り😡がいいねの数に影響しているとは言えなさそうでした…
終わりです😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡
p値を用いたTarget Encoding
こんにちは、クルトンです!
この記事では二値分類問題でのp値を用いたTarget Encodingについて説明しようと思います。
p値とは
なる検定問題において棄却域が
で与えられるとき、
をp値と言います。
簡単に説明すると「帰無仮説が正しいとした仮定とき、観測した事象よりも極端なことが起こる確率」のことです。
例えば検定統計量を「コインを投げた時に表が出た回数」とし、表と裏が出る確率が同じ(帰無仮説)とします。
このときに表が9回、裏が1回出たとすると、p値はとなります。
通常の検定では、p値が有意水準と呼ばれる基準の数値(例えば5%)を下回った場合は、これが偶然ではなく意味があることだ(有意である)と考え帰無仮説を棄却します(表と裏が出る確率が同じだという前提が間違っていたと考える)。
このように、p値を用いることによって、観測した事象がどのくらい起こりにくいかを知ることができます。
通常のTarget Encodingの欠点
通常のTarget Encodingでは、あるカテゴリに所属するデータの数が少ないと過学習の原因になってしまう可能性があります。
この問題の解決策として、TargetEncodingのスムーシングがありますが、これもハイパーパラメーターが存在するという問題点があります(スムーシングについては以下の記事を参照してください)。
そこで僕は、p値を使えばこの問題を解決できるのではないかと考えました。
p値を用いたTarget Encoding
通常のTargetEncodingは、をクラスタiに所属しているデータの数、
をクラスタiに所属していて目的変数が1の数としたとき
と表せます。
しかし、や
の値が小さいと、間接的に目的変数の値を予想できてしまうため過学習を引き起こしてしまいます。
ここでp値を用いる方法について考えてみましょう。
をデータの総数、
をデータセット全体の中で目的変数が1の数とします。
すると全体としては十分なデータ数があるとき、クラスタiの目的変数の総和はのような二項分布に従うと仮定できます(帰無仮説)。
このときの各々のクラスターでのp値を求めれば、そのクラスターが平均からどのくらい外れているかを計算できるのではないか?というのがp値を用いたTarget Encodingです。
p値の計算と連続修正
上記の変数を用いると、カテゴリiのp値はで求める事ができます。
しかしこのようにしてp値を求めると、のときに、
であればp値は
になり、
であればp値は
になってしまいます。
これは、二項分布が離散変量に基づく分布にもかかわらず、目的変数の合計値を連続変量として扱っているためです。
このような場合は、連続修正を行うことでより正確なp値を求めることができます。
具体的には上記の式においてのときに足す項を1/2倍することで連続修正をすることができます。
上記の例では、この連続修正を行うことでどちらもp値が0.5になります。

実際に使用した結果
規約により具体的なコンペの内容は説明できませんが、atmaCup13ではAdditive Smoothing Target Encodingよりもp値を用いたTarget Encodingの方がスコアが改善しました。
皆さんもぜひp値を用いたTarget Encodingを使ってみてください!
統計検定1級の勉強法(まとめノートの作り方)
こんにちは、クルトンです!
以前に統計検定1級の勉強法について記事を出したのですが、そこで勉強法として「まとめノートを作る」というものを紹介しました。
そこで、この記事ではまとめノートの作り方について詳しく説明しようと思います。
なぜまとめノートを作るのか?

これは上の記事でも説明したのですが、まとめノートを作ることには
- 分からなかった部分がまとめノート1冊にまとまっているので、2周目の解きなおしが楽になる
- テキストの内容をまとめながら読むことで、漫然と読む場合に比べてしっかりと理解できるようになる
- 「この1冊を完璧にすれば過去問は解ける」という状態を作ることで、ノートが精神的な支えになる
などのメリットがあります。
また、まとめノートは統計検定の勉強を始めたばかりの頃から作り始めても内容を理解する助けになり、逆にある程度仕上がってから作り始めたとしても自分の苦手な分野がコンパクトにまとまったノートを作る事ができるのでいつから作り始めても良いと思います。
具体的な内容
僕のまとめノートは
- 確率分布のまとめ
- 他の部分のまとめ(統計的推定、統計的仮説検定、検定統計量の導出方法、適合度検定、検定方式の評価、線形回帰モデルなど)
- 良く使う公式
- よく使う言い回し
- 用語集
- 解法パターン
- やりがちなミス
という構成になっています。
確率分布以外の部分はまとめ方が同じなので一つにまとめました。
ではここからは具体的なまとめ方について説明しようと思います。
確率分布のまとめ
僕は
- 離散一様分布
- ベルヌーイ分布
- 2項分布
- ポアソン分布
- 幾何分布
- 負の2項分布
- 超幾何分布
- 一様分布
- 正規分布
- ガンマ分布
- カイ2乗分布
- 指数分布
- ハザード関数
- ベータ分布
- コーシー分布
- 対数正規分布
- ロジスティック分布
- t分布
- F分布
について
をまとめました。
期待値や分散は母関数からも導出できますが、できるだけ直接導出できるようにもなっておきましょう(両方知っていれば簡単な方を選択できるので)。
あと、その他の性質というのは分布同士の関係性(ガンマ分布と指数分布やt分布とコーシー分布など)や指数分布の無記憶性などです。
これは確率分布曼荼羅を書いて整理してもいいと思うのですが、複雑な図を綺麗に書くのが難しいと思ったので僕はそれぞれの確率分布に書きました。
また、変数の定義域はしっかりと書いておきましょう!
他の部分のまとめ
あくまでも復習を簡単にするためのものなので、できるだけ途中式を省いて結論だけを簡潔に書きましょう。
もちろん、公式の導出方法は理解しておかなければいけませんが、それはまとめノートではなくテキストを使って勉強しましょう。
「まとめノートを見ながら導出を思い出してたら公式を覚えちゃった」みたいなのが理想だと思います。
まとめ方の一例として、『現代数理統計学の基礎』の「フィッシャー情報量とクラメール・ラオ不等式」をまとめた部分を載せておきます。

良く使う公式
過去問を解いていると、特定の公式や定理を知っている前提で出題されている問題があります。
このような式を知らなかった場合は、絶対にメモして覚えておきましょう。
良く使う言い回し
過去問を解いていると、特定の言い回しが頻繁に使われていることが分かります。
別に自分の言い回しで書いても全く問題は有りませんが、解答の書き方に詰まったときは過去問の解答の言い回しを参考にしてみると良いでしょう。
解答の言い回しまでメモするのは若干やり過ぎの気もしますが、僕は一応メモを取っていました。
(例)
- 「~の和は(分布)の全確率なので1となることを用いた。」
- 「期待値を標本平均で置き換えた形であるので
はモーメント法に基づく推定値である。」
用語集
出てきて意味が分からなかった単語をメモしていました。
解法パターン
割と統計検定の問題は解法のパターンが被っているので、解けなかった問題の解法パターンなどはメモしておくと良いでしょう。
(例)
最後に
ここまでまとめノートの作り方を書いてきましたが、これはあくまでも僕の例であり自分に合っているやり方でまとめるのが一番です。
ただ、自己満足に陥らないためにも、なぜそれをまとめる必要があるのかを意識しながらまとめノートを作ることはとても重要です。
まとめノートは作っただけでは何の意味もありませんが、自分の弱点になっている部分を的確にまとめ、それを何度も何度も読み直すことで非常に効率的に学習することができます。
まだまとめノートを作っていない方は、ぜひ一度試してみてください!
この記事が少しでも皆さんの役に立つことを願っています。
統計初学者が統計検定1級に合格する方法
こんにちは、クルトンです!
2021年11月21日に実施された、統計検定1級(数理統計、応用統計(理工学))に合格することができました!
なので、この記事では統計検定を受けるまでに勉強した内容について書こうとおもいます。
勉強を始める前の状態
- 統計はセンター試験と大学1回生のときに般教でやった程度(分散は分かるけど不偏分散って何?ぐらいのレベル)
- 高校数学は得意な方だった
みたいな感じです。統計検定は受けたことが無かったのですが、高校数学は割と得意だったので「1級をパッと取ってサクッと終わるべ!」ぐらいの気持ちで一級に申し込みました。(この頃は2~3週間勉強すればいけるだろうと思っていた)
参考書
使用した参考書を紹介します。
それぞれのテキストにかかった勉強時間と個人的なおススメ度、難易度と使用した感想を説明します。
入門統計解析
所要時間:34時間(テキストを読んで問題を一周しました)
おススメ度:★★★★☆
難易度:★★☆☆☆
感想:問題演習も豊富で初学者でも分かりやすい内容になっていました。他の入門書を買っていないので比較はできませんが、初めて統計を学ぶのならこれで問題が無い気はします。
現代数理統計学
所要時間:24時間(少しだけ読んで読了を諦めました)
おススメ度:★★☆☆☆
難易度:★★★★★
感想:とにかく難しい。数学力に自信がある人は挑戦してみてもいいかもしれませんが、僕はおススメはしません。僕は途中で理解するのを諦めて、これから紹介する『現代数理統計学の基礎』にテキストを換えました。
現代数理統計学の基礎
所要時間:74時間(1~9章を読んで、1~4章の問題を2周しました)
おススメ度:★★★★★
難易度:★★★★☆
感想:久保川本と呼ばれており、多くの1級受験者がこの本で勉強しています。この本を仕上げれば数理統計に関しては問題なく解けるようになると思います。
大学教養線形代数(数研講座シリーズ+チャート式)
所要時間:56時間(テキストを読んで問題を1周しました)
おススメ度:★★★★☆
難易度:★★☆☆☆
感想:線形代数についての知識がゼロだったので読みました。大学で線形代数の講義を受けた人は読まなくていいと思います。誤植が極めて少ないためストレスなく読めたので、初学者にはかなりおススメです。
確率と確率過程
所要時間:22時間(テキストを読んで問題を1周しました)
おススメ度:★★★☆☆
難易度:★★★☆☆
感想:応用統計(理工学)の対策のために読みました。必須というわけではありませんが、読むのにそれほど時間がかからないため応用統計が不安な方は買ってみてもいいと思います。
過去問(2012~2019)
所要時間:103時間(問題を4周しました)
おススメ度:★★★★★
難易度:★★★★☆
感想:高いですが絶対に買いましょう。解説は誤植がかなり多く証明が省略されている部分も多いため、解説を読んでも良く分からなかった部分はネットの解説記事を参考にすると良いでしょう。
やって良かったことorやっておけば良かったこと
統計検定の勉強で「これをやって良かったな」ということと、逆に「これをやっていれば良かった…」ということを書いておこうと思います。
まとめノートを作る
これは本当にやって良かったです。内容の8割ぐらいはテキストの内容をまとめただけですが、他にも問題演習で自分のやりがちなミスや覚えておくべき式(一から導出するには時間がかかるが頻出であるようなもの)、解法パターンや混同しそうな単語(有意水準と有意確率、最尤推定量と最尤推定値、etc.)などを書いていました。
メリットとしては
- 分からなかった部分がまとめノート1冊にまとまっているので、2周目の解きなおしが楽になる
- テキストの内容をまとめながら読むことで、漫然と読む場合に比べてしっかりと理解できるようになる
- 「この1冊を完璧にすれば過去問は解ける」という状態を作ることで、ノートが精神的な支えになる
などがあります。
勉強を始めたての人だけでなく、直前期の人でもまとめノートを作ることを強くお勧めします。
まとめノートの作り方については以下の記事に詳しく書いたので、良かったら読んでみてください。
過去問を早くからやる
僕は久保川本を読み終わってから過去問を解き始めたので、割と遅く(約1か月前)なってしまったのですが、もう少し早くやっておけば良かったなと思います。
僕が速くから過去問を解き始めた方が良いと思うのは
- 問題数が多いため時間がかかる(僕が受けたときは過去問が8年分あり、応用統計と数理統計がそれぞれ5問ずつ出題されるので、全部で80問ありました。)
- 問題を見ることでテキストの読み方が変わってくる(テキストではあまり強調されていない部分が頻出だったりする)
という理由です。
僕がテキストを1周したときに過去問を解いてみると、「テキストに載ってたことはなんとなく覚えてるけど全く解けない…」みたいな状態になったので、もっと早く問題を見ておけば良かったと後悔しました。
ただ正直なところ、テキストをまだ1周していない時点で過去問を見ても全く分からないと思うので、過去問1年分をテキストの演習問題として使うか、テキストを2周する前提で早くから勉強を始めるのが良いと思います。
連想ゲームをしてみる
上記の2つほど重要ではありませんが、割とおススメの勉強法として連想ゲームがあります(僕がかってに名前を付けました)。
例えば不偏分散からスタートすると
「不偏分散の不偏ってなんだっけ?」
→「なんでじゃなくて
で割るんだっけ?」
→「不偏分散の不偏性の証明ってどうするんだっけ?」
→「といえば
ってどうやって証明するんだっけ?」
みたいな感じです。
この「色んなことを思い出しながら頭の中で証明して復習する」という勉強法は記憶も定着するし、場所も問わず隙間時間に勉強できるのでおススメです。僕は通学中に自転車を漕ぎながらよく考えてました。
もちろん、頭の中で証明できなければ家に帰ってから紙に書いて解いてみるのも良いでしょう。ただ、この勉強法は記憶を定着させるのが目的なのですぐに調べてしまうのはお勧めしません。
ときどき全く新しい疑問が生まれることもあるので、そういう場合は覚えるかメモしておいて家に帰ってからじっくり調べてみると良いでしょう。
最後に
いろいろ書いてきましたが、万人に通用する勉強方法というものはないので他の人の記事も読んで色々試してみるのが良いと思います。
この記事が誰かのお役に立てれば幸いです。
Optunaでヒューリスティックコンテストを解く
この記事は競プロ Advent Calendar 2021 14日目の記事です。
こんにちは、クルトンです!
この記事ではヒューリスティックコンテストにOptunaを活用する方法について解説しています。
Optunaとは
Optunaは公式サイトで以下のように説明されています。
Optuna はハイパーパラメータの最適化を自動化するためのソフトウェアフレームワークです。ハイパーパラメータの値に関する試行錯誤を自動的に行いながら、優れた性能を発揮するハイパーパラメータの値を自動的に発見します。現在は Python で利用できます。
Optuna は次の試行で試すべきハイパーパラメータの値を決めるために、完了している試行の履歴を用いています。そこまでで完了している試行の履歴に基づき、有望そうな領域を推定し、その領域の値を実際に試すということを繰り返します。そして、新たに得られた結果に基づき、更に有望そうな領域を推定します。具体的には、Tree-structured Parzen Estimator というベイズ最適化アルゴリズムの一種を用いています。
ハイパーパラメータ自動最適化ツール「Optuna」公開
「良い感じのハイパーパラメーターを見つけてくれるPythonのライブラリ」という理解で大丈夫です。
具体的な使い方
簡単な使用例を見てみましょう。
Optunaでを最小化する
を調べてみます。
import optuna # 最小化する目的関数 def objective(trial): # パラメータ x = trial.suggest_uniform('x', -10, 10) score = (x - 2) ** 2 # 最小化したい値を戻り値にする return score # Studyを作成 study = optuna.create_study() # 目的関数をStudyに渡す study.optimize(objective, n_trials=100) # 実験で得られた最良のパラメーター print(study.best_params) # 実験で得られた最良の目的関数の値 print(study.best_value)
何をしているのかはコメントに書いてある通りなんですが、一応流れを書いておくと
- 最小化(または最大化)したいスコアを返り値とする目的関数を定義する
- optuna.studyインスタンスを作成する
- optuna.study.optimizeに目的関数を渡す
これだけです!めっちゃ簡単ですね!
ちなみに上のコードの実行結果は以下のようになりました。
{'x': 2.005349708575524}
2.861938184303352e-05
この結果を見ると、の値が
を最小化する
に十分近く、実験が上手くいっていることが分かります。
ヒューリスティックコンテストでOptunaを使う
ヒューリスティックコンテストではハイパラ調整を行う場面が数多くあります。
例えば、焼きなまし法の温度調整などです。焼きなまし法では初期温度と終点温度の2変数を使用するため、これらをハイパーパラメータとして調整することになります。
パラメーターが1つだけであれば人力でも時間を掛ければ調整できるかも知れませんが、3つ4つと増えてくると、人力でのパラメーター調整が困難*1になってきます。
そこでこのようなハイパーパラメーターの調整をOptunaにやらせよう、というのがこの記事の内容になります。
Python以外でもOptunaを使いたい!
ここまで、Optuna自体の説明とどのようにヒューリスティックコンにOptunaを活用するのかを説明してきました。
しかし、OptunaはPythonのライブラリであるため、ほかの言語で書いたコードのハイパラ調整に用いるのが難しいという問題点があります。
そのため、ここではC++で書かれたヒューリスティックコンテスト(AHC005)のコードを例に、Optunaの使い方を説明していこうと思います。(コードの使用を許可してくださったMtSakaさん、ありがとうございます)
ここでは2つのパラメーターa, bを調整してスコアの変化を調べます。(なんのパラメーターなのかという説明は本質ではないので省略します)
C++側のコード
int main(int argc, char* argv[]){ if (argc >= 4) { double a, b; string text_path; a = stod(argv[1]); b = stod(argv[2]); text_path = argv[3]; textfile_input(text_path); init(); calc_dist(); solve(a, b); initialize(); int score = round(1e4+1e7*(double)n/best_cost); cout << score << endl; } }
全体を載せると長くなりすぎるのでmain関数だけを載せました。
重要なのは
- ハイパラと使用するテストケースのパス*2を受け取る
- スコアを返す
という二点だけです。
textfile_inputはテストケースのパスを渡すと入力を受け取るような関数になっています。
Python側のコード
import optuna import subprocess from multiprocessing import Pool import os import optuna from random import sample from tqdm import tqdm using_testcase_num = 200 total_testcase_num = 10000 n_trials = 400 def f(args): i, a, b = args cmd = './a.out {} {} in/{:04}.txt'.format(a, b, i) res = subprocess.run([cmd], universal_newlines=True, shell=True, stdout=subprocess.PIPE) return float(res.stdout) def wrapper(args): mean = 0 using_tastcases = sample(list(range(total_testcase_num)), using_testcase_num) with Pool() as pool: mean = sum(pool.map(f, [[i] + args for i in using_tastcases])) mean /= using_testcase_num return mean def objective(trial): a = trial.suggest_loguniform('a', 1e-8, 1e8) b = trial.suggest_loguniform('b', 1e-8, 1e8) score = wrapper([a, b]) print('a: %1.3f, b: %1.3f, score: %f' % (a, b, score)) return score # 探索 study = optuna.create_study(direction='maximize') study.optimize(objective, n_trials=n_trials) print('best_score:{:.2f}'.format(study.best_value)) print('a:{}, b:{}'.format(study.best_params["a"], study.best_params["b"])) # logの書き込み f = open('log.txt', 'a') f.write('best_score:{:.2f}, a:{}, b:{}, using_testcase_num:{}, total_testcase_num:{}, n_trials:{}\n'.format(study.best_value, study.best_params["a"], study.best_params["b"], using_testcase_num, total_testcase_num, n_trials)) f.close() # 探索過程の可視化 fig = optuna.visualization.plot_optimization_history(study) fig.show()
この部分は真紅色に染まるぷーんさんのコードを参考にさせて頂きました。ありがとうございます。
結構長いコードなので、いくつかに区切って解説していきます。
ライブラリのインポート
import optuna import subprocess from multiprocessing import Pool import os import optuna from random import sample from tqdm import tqdm
ライブラリをインポートしているだけですね。
各種変数
using_testcase_num = 200 total_testcase_num = 10000 n_trials = 400
いくつかの変数を定義しています。
今回のコードでは
- optunaが1回の探索に用いるテストケース数
- 用意している総テストケース数
- optunaの探索回数
を定義しています。
目的関数
def f(args): i, a, b = args cmd = './a.out {} {} in/{:04}.txt'.format(a, b, i) res = subprocess.run([cmd], universal_newlines=True, shell=True, stdout=subprocess.PIPE) return float(res.stdout) def wrapper(args): mean = 0 using_tastcases = sample(list(range(total_testcase_num)), using_testcase_num) with Pool() as pool: mean = sum(pool.map(f, [[i] + args for i in using_tastcases])) mean /= using_testcase_num return mean def objective(trial): a = trial.suggest_loguniform('a', 1e-8, 1e8) b = trial.suggest_loguniform('b', 1e-8, 1e8) score = wrapper([a, b]) print('a: %1.3f, b: %1.3f, score: %f' % (a, b, score)) return score
実行を並列化をしているのでコードが複雑になっていますが、一つずつ見ていけば大して難しくありません。
まずf(args)ですが、この関数ではテストケースの番目を表すiと最適化させたい2つのパラメーターa,bを受け取り、パラメーターa,bでテストケースiを実行した際のスコアを返しています。このときに、subprocess.runで先程コンパイルした./a.outを実行しています。
次にwrapper(args)では、2つのパラメーターa,bを受け取り、用意しているすべてのテストケースから1回の探索に用いる分のテストケースを抽出し、パラメーターa,bでそれらを実行した際のスコアの平均を返しています。
最後に目的関数ですが、これは単純にwrapper(args)の返り値をそのまま返しています。
探索
study = optuna.create_study(direction='maximize') study.optimize(objective, n_trials=n_trials) print('best_score:{:.2f}'.format(study.best_value)) print('a:{}, b:{}'.format(study.best_params["a"], study.best_params["b"]))
パラメーターを探索しています。今回はスコアが高ければ高いほど良いという問題設定だったので、optuna.create_studyの引数に direction='maximize' を渡すことで目的関数の返り値を最大化させています。
logの書き込み
f = open('log.txt', 'a') f.write('best_score:{:.2f}, a:{}, b:{}, using_testcase_num:{}, total_testcase_num:{}, n_trials:{}\n'.format(study.best_value, study.best_params["a"], study.best_params["b"], using_testcase_num, total_testcase_num, n_trials)) f.close()
探索結果をテキストファイルに書き込ませています。
探索過程の可視化
fig = optuna.visualization.plot_optimization_history(study) fig.show()
探索過程をグラフとして表示させています。
以上がコードの説明になります。
実験結果
実際に
- using_testcase_num:100
- total_testcase_num:10000
- n_trials:400
で実験してみたところ
以下のような結果になりました。

縦軸が目的変数、横軸が最適化の探索回数になってます。オレンジの折れ線が最良の目的変数の値となっており、何回目のトライアルでベストパラメータが出たのかが分かるようになっています。
上のグラフから
- 100回探索した時点でスコアがかなり収束していること
- パラメーターによってスコアが大きく変動すること
などが分かります。
スコアを最大化するように調整したパラメーターで実際に提出してみたところ、21707556点でした。
また一方で、スコアを最小化するように調整した*3パラメーターで提出したところ、4235639点になりました(上記のスコアの約5分の1)。
このことから、実験は上手くいっており、Optunaを使ってパラメーターを調整することで大きくスコアが改善できるということが確認できました。
おまけ
ここまで書いておいてなんですが、実は今回の実験では元々のコードのスコアを超える事ができませんでした…


探索回数(n_trials)を1000~2000回まで増やして回すことも考えたんですが、そこまで探索に時間をかけるのは「Optunaで手軽にハイパラを調整する」という本来の目的から外れているように思えたので、残念ですがここで断念しました。
しかも話を聞くと、MtSakaさんは3回の探索でこのスコアを出したらしいです…(は?)
MtSakaさんがOptunaより強いということが分かったところで、この記事を終わらせて頂こうと思います!それではまた!
atmaCup参戦記(#11)
こんにちは、クルトンです!
この記事は僕が参加したatmaCup#11の参戦記になります。
この記事ではコンペ中に僕がどのようなことを考え、何をしていたのかということをメインに書こうと思っています。
なので、良いスコアが出る解法を知りたいという方にはツヨツヨの人たちの解法記事を見ることをお勧めします。
- コンペが始まる前
- コンペ開始(7/9)
- BERTを使う(7/10)
- nyk_gotoさんのコードをイジり始める(7/11)
- sorting_dateをtargetに変換する(7/12)
- ttaを試してみる(7/13)
- 他のモデルを試してみる(7/14)
- ひたすら学習を回す(7/16~7/20)
- part5とpart6をアンサンブルする(7/21)
- 結果
コンペが始まる前
サムネイルの画像から、今回のコンペも絵画がテーマになるということが分かっていたので、絵画から文章を作成して、特徴量にするコードを書いていました。
ネットから拾ってきたのを少し変えただけですが、割とうまく行っていたのでワクワクしながらコンペが始まるのを待っていました。

かなり正確に絵画の内容を説明できていることが分かる。
結局、事前学習済みのモデルが使えないということだったのでこれは使えませんでしたが、楽しかったし割といい勉強にもなりました。
コンペ開始(7/9)
いよいよコンペが始まりました。
次の日に開催されるnyk_gotoさんの初心者講座でベンチマークとなるコードがもらえるのは分かっていたのですが、とりあえず自力で1subできるように頑張ってみようと思いました。
このときは、スコアは気にせず1subすることを目的としていたので大分特殊な解法で解いていました。
(SimSiamによる自己教師あり学習チュートリアル(https://www.guruguru.science/competitions/17/discussions/a39d588e-aff2-4728-8323-b07f15563552/)によって得た情報を、16次元に落とし、そこからLGBMを使って回帰予想するというもの)
このときのスコアは、(CV:0.9377, LB: 0.9340)とかなり悪いものでしたが、スコアが出るコードを自分で書けたというのが初めてのことだったのでとても嬉しかったことを覚えています。
BERTを使う(7/10)
ほぼ一日かけて
- Trainデータのmaterial, techniquesをBERTの2次元ベクトルに直す
- 16次元に落とした画像情報からtrainデータのBERTベクトルを学習させ、テストデータのBERTベクトルを予測する。
- 16次元に落とした画像情報と予想したBERTベクトルから年代を予測する。
ということをしました。
結果は(CV: 0.8463, LB: 0.9607)でCVがめちゃくちゃ改善したので期待しましたが、LBではむしろスコアが悪化してしまいました(絶対上がると思ったので結構ショックでした)。
そしてなぜこのような結果になったか考えて
- material, techniques のBERTは効く
- このやり方ではテストデータのBERTを正確に予測することができない
という結論に至りました。
とりあえずこの日はこの作業で終わって、次の日から大人しくnyk_gotoさんのコードを使って取り組むことにしました。
nyk_gotoさんのコードをイジり始める(7/11)
nyk_gotoさんのコードを使って
- epoch=30
- StratifiedGroupKFold(n = 5)
で学習させました(以下、この実験をpart1とする)。
結果は(CV: 0.8928, LB: 0.8902)でした。
0.8台にのったことは嬉しかったのですが、この時点で上位陣は軒並み0.7台だったので、単純なことを見落としているんだろうな~と思っていました。
そこで、絵画の場合は色彩が重要なのではないかと思い、data augmentationでの色や明度彩度の変換をなくすことにしました(以下、この実験をpart2とする)。
これによって(CV: 0.8694, LB: 0.8591)まで上がりました。
ただ、これでも0.7台には程遠いので、単純にepoch数が足りないのではないかと考えました。
そこで、part2のepochを100まで増やしたところ、スコアが(CV: 0.8200, LB: 0.8370)まで改善しました。
sorting_dateをtargetに変換する(7/12)
どうせ回帰分析をするなら、sorting_dateを回帰したほうが精度が上がるのではないかと思い、sorting_dateをtargetに変換して回帰を行いました。
その際、part2のtargetをsorting_dateにしたもの(part3)とpart1のtargetをsorting_dateにしたもの(part4)で実験を行いました。以下はその結果です。
- part1, epoch = 300: (CV: 0.7794)
- part1, epoch = 400: (CV: 0.7654, LB: 0.7543)
- part3, epoch = 200: (CV: 0.7777)
- part4, epoch = 100: (CV: 0.8429)
ttaを試してみる(7/13)
part3がうまく行きそうだったのでそのまま学習を進めました。
- part3, epoch = 400: (CV: 0.7456, LB: 0.7386)
学習を回している間が暇だったので、part3にttaを試してみることにしました。
- part3, epoch = 400, tta: (CV: 0.8534, LB: 0.7355)
このときにCVが謎の下がり方をしてメチャクチャ焦りました…(未だに原因が分かっていないとは言えない)
他のモデルを試してみる(7/14)
part3がうまく行っていることは分かったので、ディスカッションで話題になっているモデルを試してみる事にしました。
ひとまず、part3のモデルだけをEfficientNet0Bに変えたpart5を作って学習を回すことにしました。
- part5, epoch = 400: (CV: 0.7390, LB: 0.7105)
- part5, epoch = 500: (CV: 0.7355, LB: 0.6950)
このときは、最終的には0.67当たりの勝負になると思っていたのでかなり喜んでいました。
今から思うと、これぐらいのスコアでも充分勝負になるだろうと思い、ほかの手法に積極的に手を出さなかったのが良くなかったのだと思います。

ひたすら学習を回す(7/16~7/20)
part3のモデルをresnet-18に変えたpart6を作りました。
この期間は脳死でpart5とpart6の学習を延々と回していました。
今から考えると、完全にこの期間何もしていなかったのが敗因だったんだな~と思います…
この時点でのスコアは以下の通りでした。
- part5, epoch = 700, tta = 100: (CV: 0.7076, LB: 0.6947)
- part6, epoch = 1500, tta = 100: (CV: 0.7101, LB: 0.7094)

part5とpart6をアンサンブルする(7/21)
- part6とpart7のアンサンブル, tta = 100: (CV: 0.6846, LB: 0.6938)

このときは、アンサンブルがかなり効いたのが嬉しかったのと同時に、「もしかしてSimSiamの方も回してればアンサンブルでワンチャンあった?」と思いかなりへこみました。
最終日になって途中まで回していたSimSiamの学習を再開したのですが、当然間に合いませんでした…
結果

614チーム中22位という結果に終わりました。
実力以上の結果を出せたとは思いますが、内容としてはかなり反省点が多いコンペだったので次に活かそうと思います。